|
Calculation:
Compute
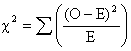
There are 16 observed frequencies (O) and 16 expected frequencies (E). As in the case of the goodness of fit, calculate this c2 value. In our case, the computed c2 =131.76 as shown below: Each cell in the table below shows (O-E)^2/(E)
|
Brand1 |
Brand2 |
Brand3 |
Brand4 |
| Income |
|
|
|
|
| Lower |
8.20 |
21.49 |
14.08 |
23.36 |
| Middle |
0.27 |
2.86 |
4.00 |
0.33 |
| Upper Middle |
2.27 |
3.43 |
3.69 |
3.71 |
| Upper |
3.24 |
17.30 |
12.28 |
11.25 |
And there are 16 such cells. Adding all these 16 values, we get c2 =131.76
The critical value of c2 depends on the degrees of freedom. The degrees of freedom = (the number of rows -1) multiplied by (the number of columns -1) in any contingency table. In our case, there are 4 rows and 4 columns. So the degrees of freedom = (4-1). (4-1) =9. At 5% level of significance, critical c2 for 9 d.f = 16.92. Therefore, reject the null hypothesis and accept the alternative hypothesis.
The inference is that brand preference is highly associated with income level. Thus, the choice of the brand depends on the income strata. Consumers in different income strata prefer different brands. Specifically, consumers in upper middle and upper income group prefer premium brands while consumers in lower income and middle-income category prefer economy brands. The company should develop suitable strategies to position its detergent products. In the marketplace, it should position economy brands to lower and middle-income category and premium brands to upper middle and upper income category.
Concluded.
Back to main page
* * Prof. P.K. Viswanathan is an Adjunct Professor and Management Consultant based in Chennai, India.
|
 |
 |
|